미분방정식 급수해법

시험정리용

증명없음

개념은 문제 풀 때 필요한 부분만 언급해서 개념과 많이 다를 수 있음

글에서는 x=0일때만 다룸

 

 

 

이런 꼴로 미분방정식이 있고, p(x), q(x), r(x)가 analytic function일 때 멱급수를 사용하면 쉽게 풀리는 경우가 있다.

수업에서는 거의 다 x=0일때에서만 배웠는데, x=x0인 경우 t = x-x0로 치환해서 풀면 된다.

 

 

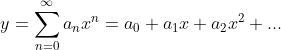
기본 문제 풀이는 2가지로 나뉜다.

 

y = (시그마가 들어있는 식) = (전개 식)

 

이렇게 있으면 시그마가 들어있는 식으로만 정리해서 풀거나, 어떻게 생긴 급수인지 유추가 불가능할 경우엔 전개 식을 사용하여 풀면 된다.

 

==========================================================================

 

 

-Frobenius Method

 

이런 꼴로 표현이 가능할 때 x = 0에서 불연속이지만 b(x), c(x)가 analytic function일 때 사용하는 방법이다.

x = 0에서 연속일때도 사용할 수 있지만 프로베니우스는 r을 구하는 과정이 추가되었기 때문에 그냥 멱급수로 푸는게 시간이 더 단축된다.

 

 

맨 위에 있던 y에 x^r을 곱하여 풀면 된다.

 

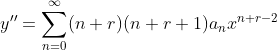
이 식들을 대입하여 정리한 후에 n=0일때 x의 최소차항이 몇인지 구한다.

그리고 n=0일때 x의 최소차항이 될 수 있는 항들만 모아서 계산한다음 r의 값을 구하면 된다.

 

중근을 제외하면 r = r1, r2가 나올텐데 r1 > r2, r1 - r2 = n(n은 정수)일 때

y1부터 구한다면 r = r1을 대입하여 시그마 식을 싹다 정리시킨다음, 차수를 s로 전부 치환시켜 통일시키고 점화식을 구한다.

점화식을 구했다면 간단한 식이 나오거나 매클로린 급수(crush-on-study.tistory.com/93)를 구하여 y1을 구한다음

y2 = uy1을 이용하여 푸는 Reduction of Order를 이용하여 y2를 구하면 된다.

 

 

글은 쓸게 별로 없지만 풀이가 너무 길다. 문제 하나에 A4 한 면을 다 쓰는 수준이다.