연립 미분 방정식(라플라스 변환)

증명없음

시험정리용

 

 

연립 미분 방정식(일반) - hello70825.tistory.com/169

 

 

 

 

 

이 식에서 그대로 라플라스 변환을 해주면 된다.

 

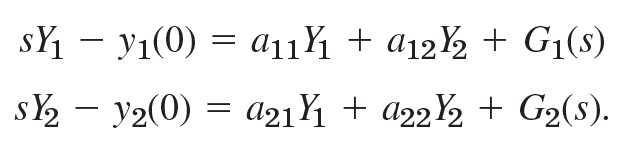
여기서 Y1, Y2를 왼쪽으로 옮기고 나머지는 오른쪽으로 옮겨서 정리하면 된다.

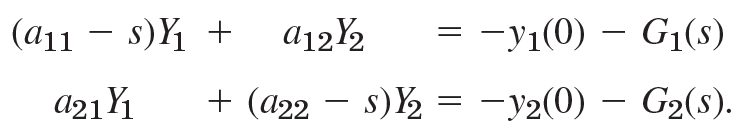
이러면 Y1과 Y2가 미지수인 일차 연립방정식이 나오므로 Y1의 값과 Y2의 값을 구할 수 있다.

그러고나서 라플라스 역변환을 해주면 y1, y2를 구할 수 있다.

 

y1'이 아닌 y1''로 나온다면 거기에 맞게 라플라스 변환을 해서 구해주면 된다.

부분분수 구하는 계산이 조금 더러울 뿐이지 개인적으로 일반적인 방법으로 연립 미분방정식을 푸는 것보다 풀기 쉬운 것 같다.