-
연립 미분 방정식(일반)학교 수업/1-2 공학수학1, 확률통계론 2020. 11. 19. 16:51반응형
증명없음
시험공부용
연립 2차 미분방정식은 지금까지 배운 미분방정식 풀이방법을 이용하거나, 라플라스 변환을 이용해 푸는 방법이 있다.
라플라스 변환은 이제 막 배우기 시작해서 나중에 글을 쓸 예정이다.
연립방정식도 Homogeneous, Nonhomogeneous 두가지로 나뉜다.
1. Homogeneous
=====================================================================
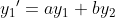
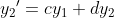
두 식이 있을 때
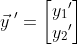
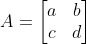
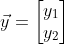
로 두어
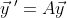
요 모양으로 만들어서 문제를 푼다.
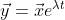
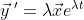
를 넣어 정리하면
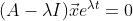
인데 eλt는 무조건 양수이므로 없애준다.
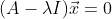
여기서 det(x) != 0이므로 det(A-λI) = 0이어야 한다.
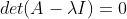
그러면 λ 값을 2개 구할 수 있다.
각각 저 식에 λ값을 대입해서 x의 값을 2개 구하면 된다.
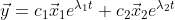
그리면 위와 같은 식을 얻을 수 있다.
============================================================================
2. Nonhomogeneous
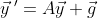
Homogeneous식과 다르게 g가 생겼다. g는 r(x)라고 생각하면 된다.
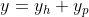
연립방정식 역시 Nonhomogeneous면 y = yh + yp로 해를 구해야한다.
그리고 yp를 구할 때는 그냥 미분방정식처럼 Undertermined Coefficients와 Variation of Parameters로 나뉜다.
Undetermined Coefficients는 푸는 방법이 비슷하지만, Variation of Parameters는 푸는 방법이 좀 다르다.
========================================================================
2-1. Undetermined Coefficients
Undertermined Coefficients는 원래 쓰던 미방처럼 푸는 것과 비슷하다.
살짝 다른점이 뭐냐면
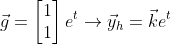
이렇게 g에 et가 있어서 yp가 uet가 되야하는데, yh가 ket인 경우
yp는 uet + vtet로 풀어줘야한다.
그냥 미방에서는 yh = ket라면 yp = vtet로 풀었지만 여기서는 해를 구할 때 상수 c가 u를 전부 흡수하지 못하기 때문에 uet + vtet로 풀어야한다.
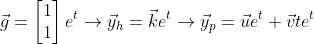
여기에 있는 yp값을
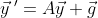
여기에 대입해서 u와 v를 구하면 된다.
========================================================================
2-2. Variation of Parameters
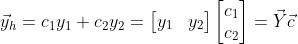
먼저 yh를 구하고 나서 yh = Yc로 Y를 빼오고, 거기에 u를 곱하면 yp라고 한다.
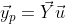
u는 어떻게 구하냐면
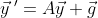
여기에 yp를 대입한다.
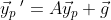
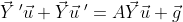
인데 Y' = [y1' y2']로 homogeneous의 해인 yh와 같으므로 Y' = AY를 넣어준다.
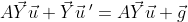
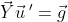
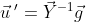
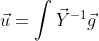
로 우리는 Y의 값과, g값을 알고 있으니 u값을 구할 수 있다.
u값을 구하고 식 yp = Yu에 대입해주면 끝난다.
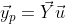 반응형
반응형'학교 수업 > 1-2 공학수학1, 확률통계론' 카테고리의 다른 글
연립 미분 방정식(라플라스 변환) (2) 2020.11.26 라플라스 변환 (0) 2020.11.25 미분방정식 급수해법 (0) 2020.11.24 고차 미분방정식 (0) 2020.11.18 1차 미분방정식 (0) 2020.11.17