1차 미분방정식

증명없음

시험정리용

 

 

1.3 Separable ODEs

 

=======================================================================

 

 

꼴로 ODE를 정리할 수 있을 때

 

 

로 만들고, dx를 오른쪽항으로 옮겨서 양변에 적분을 해준다.

 

 

 

=======================================================================

 

 

 

꼴로 ODE를 정리할 수 있을 때

 

 

로 u'x + u = f(u)로 문제를 풀어준다.

 

푸는 방법은 위에 양변을 적분해주는 것과 똑같다.

 

=======================================================================

 

 

 

 

 

1.4 Exact ODEs, Integrating Factor

 

=======================================================================

 

 

이런꼴로 문제가 있을 때에는

 

 

위와 같이 u(x,y)에 x에 대한 편미분을 하면 M(x,y), u(x,y)에 y에 대한 편미분을 하면 N(x,y)라고 해줌

 

 

이러면 위와 같은 식이 성립함

 

 

- u(x, y) 구하기

 

u(x,y)는 M을 적분하거나 N을 적분하여 구할 수 있음

 

 

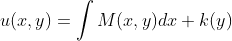
보통 M(x,y)를 적분하고 k(y)를 구함

 

k(y)를 구하는 방법은

 

 

위와 같이 integral(M(x,y))를 풀고 y에 대해 편미분을 하면 k(y)를 구할 수 있음

l(x)를 구하는 방법도 똑같음

=======================================================================

 

 

 

위와 같은 식이 있고

 

 

P와 Q를 u에 대해 편미분한 식으로 정하려고 했지만

 

 

로 편미분한 값이 서로 다를 때 적절한 Integrating Factor -> F(x) or F(y) 를 식에 전부 곱함

 

 

 

 

F(x)와 F(y)를 구하는 식은 위와 같은데 주로 F(x)를 곱하여 사용함

 

F(x)를 구했다면 양변에 곱해줌

 

 

 

위 식이 성립함

 

이것을

 

 

로 FP와 FQ를 각각 M과 N으로 변경하게되면 아래 3가지 식이 성립함

 

 

 

1.4 처음에 설명했던 식과 똑같아서 문제를 풀 수 있음

 

=======================================================================

 

 

 

 

__________________________________________________________________________________

1차 미분방정식은 아래와 같이 크게 2가지로 나뉨

 

 

r(x) = 0이면 homogeneous, r(x) != 0이면 nonhomogeneous라고 부름

__________________________________________________________________________________

 

 

 

 

 

1.5 - 1 Homogeneous Linear ODE

=======================================================================

 

 

=======================================================================

 

 

 

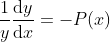
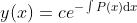
1.5 - 2 Nonhomogeneous Linear ODE

=======================================================================

 

 

1.4에서 나온 Integrating Factor를 구해서 곱해줌

 

 

=======================================================================

 

 

 

 

1.5 - 3 Bernoulli Equation

=======================================================================

 

 

이런 식이 있을 때

 

 

로 치환해서 쉽게 풀 수 있음

 

 

 

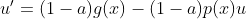
이렇게 정리하면 1.5-2 Nonhomogeneous ODE에 나온 식과 똑같은 형태라서 문제를 풀 수 있음

=======================================================================