8. NAT, IPv6, ICMP, Routing Algorithm

---

이 글은 Computer Networking: A Top-Down Approach 7th를 읽고 정리한 글입니다.

---

 

 

 

1. 네트워크 주소 변환 (NAT)

---

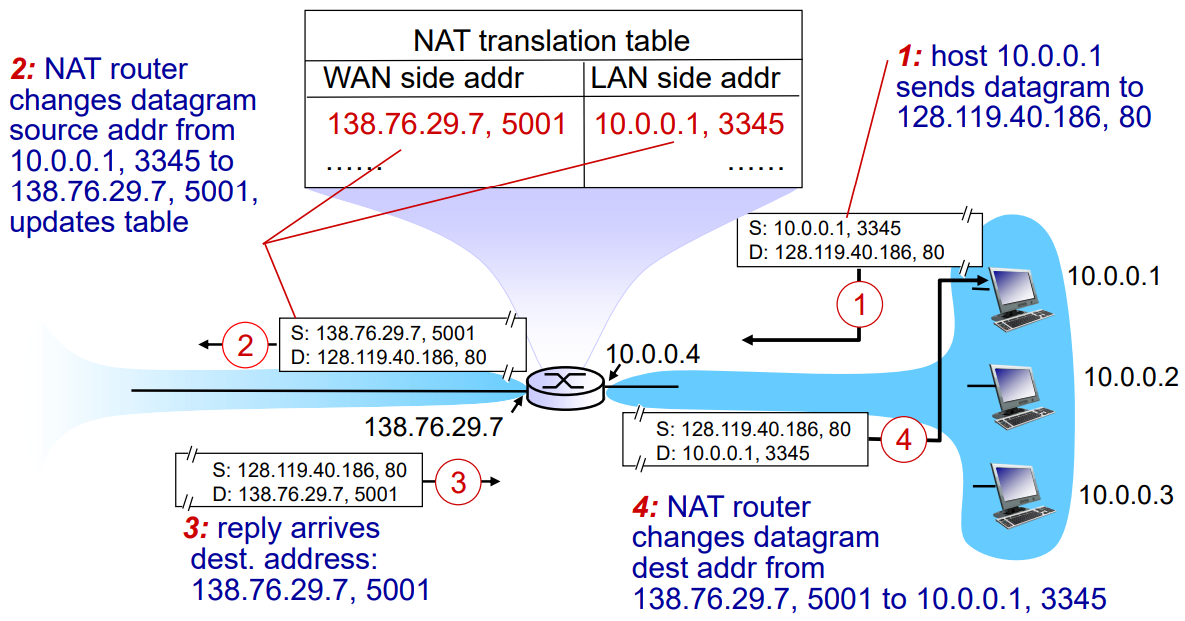
한 구역의 네트워크는 사설망을 이용하여 10.0.0.X로 서로 소통하게 만드는 것이다.

이럴 경우 하나의 IP 주소로 모든 것을 해결할 수 있다. 이때 외부와 소통을 하려면 무조건 라우터를 통해 패킷을 주고 받는다.

외부에 있던 정보가 내부로 들어와서 전달을 해야한다면 NAT 변환 테이블을 사용하여 내부 호스트에 전달을 한다.

---

 

 

 

2. IPv6

---

가정마다 최소 1대씩은 PC가 생기니까 IPv4는 2011년에 고갈되버렸고, 고갈되기전에 IPv4의 다음 버전인 IPv6이 개발이 시작되었다.

---

1) IPv6의 데이터그램 포맷

추가된 점

1. 확장된 주소: IPv4에서는 32bits였던 주소를 IPv6에서는 128bits로 확장했다.

2. 헤더: 헤더의 길이를 40바이트로 고정하여서 라우터가 더 빠르게 데이터를 처리할 수 있도록 하였다.

3. flow label: 오디오/비디오와 같이 품질/실시간 서비스는 한 흐름으로 생각하여 그 흐름의 패킷 레이블링을 한다.

없어진 점

1. 단편화/재결합: 이 기능은 시간이 오래 걸리므로 IPv6에서는 삭제한 뒤, 종단 시스템에서 작동을 수행하도록 한다.

2. 헤더 체크섬: IPv4는 거쳐가는 라우터마다 모두 체크섬을 진행하여 오래 걸렸기에 폐기하고, TCP/UDP만 하도록 한다.

3. 옵션: 더 이상 표준 IP 헤더 필드가 아니므로 40bits의 고정된 크게의 헤더를 가지게 됐다.

 

-> 속도 향상을 위해 새로운걸 추가하고 기존 것을 삭제하였다.

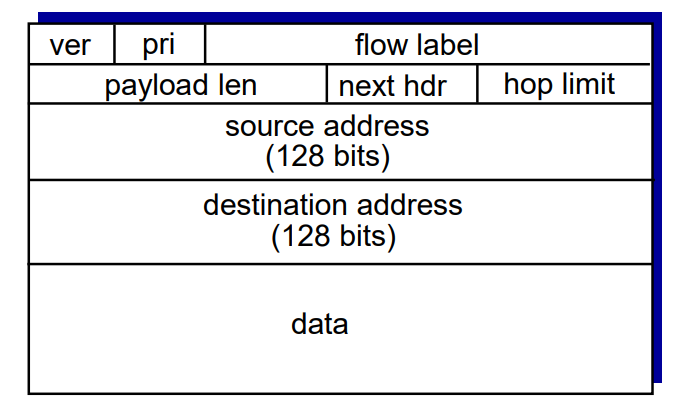
1. ver: IP 버전 번호를 뜻한다. IPv4는 4, IPv6은 6이다.

2. pri: 데이터그램에 우선 순위를 부여하는데 사용한다.

3. flow label: 데이터그램의 흐름을 인식한다.

4. payload len: 헤더 부분을 제외한 나머지 길이를 말한다. (데이터 길이도 포함)

5. next hdr: TCP와 UDP를 구분할 때 사용한다.

6. hop limit: 라우터를 최대 몇 번 거칠 수 있는지 설정한다.

7. source address, destination address: 시작/도착 주소

8. data: 데이터, payload에 속한다.

---

2) IPv4에서 IPv6으로의 전환

IPv4에서 IPv6으로 바꾸는 방법중에 하나는 인터넷 장비를 끄고 IPv4를 업그레이드하는 방법도 있지만, 상식적으로 말도 안되는 일이다. 그래서 실제로 널리 사용하는 방법은 터널링이다.

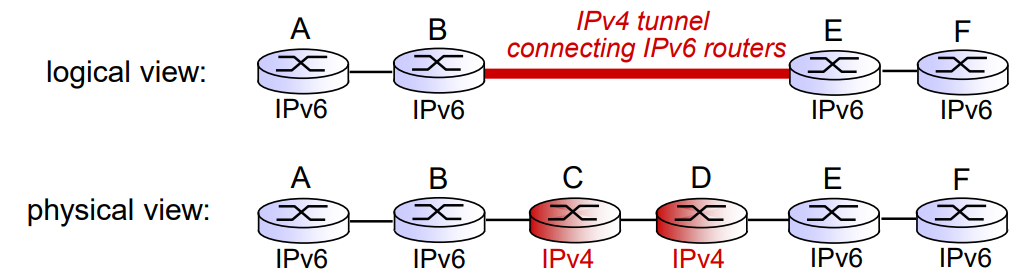
IPv4 라우터인 C와 D를 터널이라고 부르고, A에서 F로 데이터를 보내려고 한다.

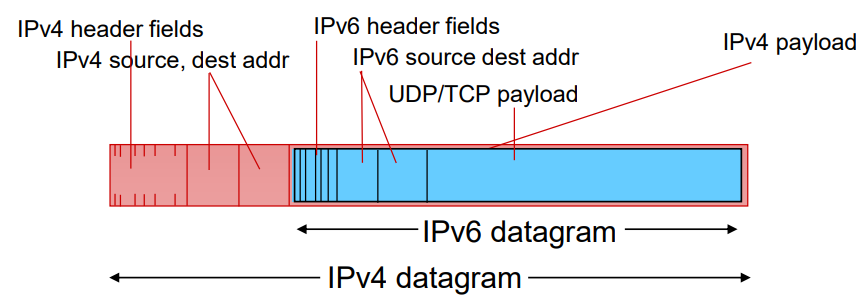
위 사진처럼 IPv4의 데이터그램이 IPv6의 데이터그램보다 크기 때문에 IPv4의 데이터 필드에 IPv6 데이터그램을 넣는다. (캡슐화)

이러면 IPv4 라우터는 해당 데이터그램이 IPv4인줄 알고 전달을 하게 되고, 다시 라우터 E부터는 IPv6으로 데이터를 전송하게 된다.

---

 

 

 

3. Internet Control Message Protocol(ICMP)

---

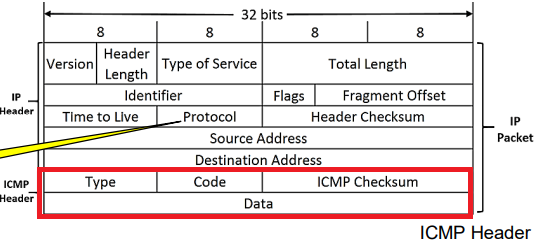
IP는 체크섬이 맞지 않으면 바로 패킷을 버리게 된다. 그리고 다시 처음부터 데이터를 받아야 한다.

그래서 네트워크 계층에서 호스트, 라우터에서 정보를 주고 받을 수 있게 만든 것이 ICMP이다.

ICMP는 IPv4에서 Protocol 필드의 값이 1이며, 값이 1인 경우 데이터 밑에 ICMP 메시지 필드값이 추가된다.

Type과 Code 값을 통해 어떤 일이 발생하는지 알 수 있다.

---

 

 

 

4. Routing Algorithm

---

네트워크에서 가장 중요한 부분이라고 할 수 있는 라우팅 알고리즘이다.

[용어 정리]

라우터 = 노드

링크 = 엣지

토폴로지 = 네트워크를 그래프로 시각화

부정적인 의미 = 코스트가 높다

 

 

라우터는 중앙 집중 혹은 분산으로 크게 두 가지의 유형으로 나눌 수 있다.

1) global

모든 링크와 라우터의 상태를 알고 있어야 한다.

모든 정보를 알고 있을 경우에는 link state 알고리즘을 사용한다.

 

2) decentralized

각 라우터는 링크로 연결된 이웃 라우터와 링크의 코스트만 알고 있다.

distance vector 알고리즘을 사용한다.

반복적으로 학습할수록 효율적인 경로를 도출해낸다.

 

또는 라우터가 정적이냐 동적이냐로도 나눌 수 있다.1) static라우터가 추가되고 삭제되는 것이 굉장히 천천히 일어난다.

 

2) dynamic라우터가 추가되고 삭제되는 것이 빠르게 일어난다.주기적으로 업데이트를 해야한다.

 

---

4.1) Link State Routing Algorithm (LS)

네트워크에서는 LS 알고리즘이라고 부르지만, 우리가 많이 알고 있는 다익스트라 알고리즘을 사용한다.

위에서 언급했듯이 모든 라우터와 링크에 대한 정보를 모든 노드(라우터)가 알고 있는 상황이다.

그래서 모든 정보를 알고 있으니 최적의 경로를 계산할 수 있으므로 포워딩 테이블을 만들 수 있다.

 

- c(x, y): x → y로 가는데 필요한 비용. 서로 연결이 안되어 있으면 무한대로 취급한다.

- D(v): 출발지에서 노드 v까지 가는데 필요한 최소 비용

- p(v): 출발지에서 노드 v까지 최소 비용으로 가는데, v에 도착하기 직전에 방문해야할 노드

- N': 노드의 집합 (모든 노드가 N'에 속하게 되면 알고리즘 종료)

 

이제 수도 코드를 살펴보자

먼저 초기화부터 살펴보자.

2: 시작 노드는 u로 N'에 노드 u를 넣어준다.

3: 모든 노드에 대해 for문을 돌리고, 이때 각 노드의 이름을 v로 한다. (우리가 for문 돌리면 i로 설정하는 것처럼)

4: 만약 v와 u가 이웃 노드라면

5: D(v) 값을 c(u, v)로 설정한다.

6: v와 u가 이웃 노드가 아니라면 D(v) 값을 무한대로 설정해둔다.

 

8 ~ 15: N'에 모든 노드가 들어갈 때까지 반복문을 돌린다.

9: 어떤 노드 w가 N'에 속하지 않고, D(w)의 값이 최솟값이 될 때

10: 노드 w를 N'에 추가한다

11: w와 인접한 모든 노드 v에 대해 업데이트를 진행한다. 

12: 출발지에서 노드 v까지 가는 경로의 코스트(D(v))와 출발지에서 노드 w까지 간 후 w → v로 가는 경로를 서로 비교하여 작은 값을 D(v)로 설정한다.

 

여기서 우선순위 큐에 대해서는 언급되지 않았지만, 다음 노드를 선택할 때는 아직 N'에 들어가지 않았지만 최소 비용 값을 가지고 있는 노드를 선택하게 된다.

---

4.2) Link State Routing Algorithm 예제

수도 코드만 보면 어려울 수도 있으니 직접적으로 예시를 들어보자

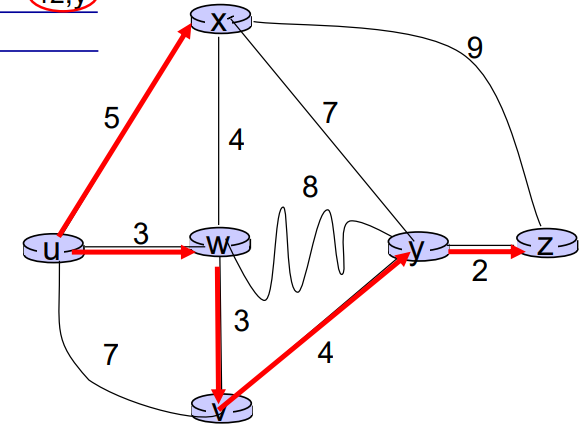
노드 u에서부터 시작한다고 해보자

u → v를 계산하면 cost는 7이므로 D(v) = 7이고, v로 가는 직전의 노드는 u이므로 p(v) = u이다.

u → y를 계산하면 서로 연결된 것이 없으므로 D(y) = 무한대이다.

그래서 u를 제외한 모든 노드에 대해 계산하면 아래 표가 나온다.

Step	N'	D(v), p(v)	D(w), p(w)	D(x), p(x)	D(y), p(y)	D(z), p(z)
0	u	7, u	3, u	5, u	∞	∞

이제 여기서 최소 비용 경로를 가지는 w를 보자

w는 아직 N'에 속하지 않았으니 w에서 시작을 할 수 있게 된다.

Step	N'	D(v), p(v)	D(w), p(w)	D(x), p(x)	D(y), p(y)	D(z), p(z)
0	u	7, u	3, u	5, u	∞	∞
1	u, w	6, w		5, u	11, w	∞

w → v를 생각해보면 기존에 u → v로 가는 것보다 u → w → v로 가는 것이 더 비용이 적게 들기 때문에

D(v) = min(D(v), D(w) + c(w, v)) = min(7, 3 + 3) = 6으로 업데이트한다.

마찬가지 방법으로 w → y로 가는 길도 있으니 y를 업데이트 한다.

여기서 가장 적은 비용을 가진 것은 x이므로 N'에 x를 추가하여 시작한다.

Step	N'	D(v), p(v)	D(w), p(w)	D(x), p(x)	D(y), p(y)	D(z), p(z)
0	u	7, u	3, u	5, u	∞	∞
1	u, w	6, w		5, u	11, w	∞
2	u, w, x	6, w			11, w	14, x

가장 적은 코스트를 가진 v를 N'에 추가한다.

Step	N'	D(v), p(v)	D(w), p(w)	D(x), p(x)	D(y), p(y)	D(z), p(z)
0	u	7, u	3, u	5, u	∞	∞
1	u, w	6, w		5, u	11, w	∞
2	u, w, x	6, w			11, w	14, x
3	u, w, x, v				10, v	14, x

가장 적은 코스트를 가진 y를 추가한다.

Step	N'	D(v), p(v)	D(w), p(w)	D(x), p(x)	D(y), p(y)	D(z), p(z)
0	u	7, u	3, u	5, u	∞	∞
1	u, w	6, w		5, u	11, w	∞
2	u, w, x	6, w			11, w	14, x
3	u, w, x, v				10, v	14, x
4	u, w, x, v, y					12, y

마지막 남은 z를 추가하면서 link state 알고리즘은 끝나게 된다.

---

4.3) Distance Vector Routing Algorithm (DV)

DV 알고리즘은 벨만-포드 알고리즘을 사용한다.

벨만 포드 알고리즘은 다익스트라 알고리즘처럼 최단 거리를 구하는 알고리즘이지만, LS 알고리즘과 큰 차이점은 위의 표처럼 남은 노드중에서 가장 작은 코스트를 가지는 노드를 선택해야 할 때, 이웃 노드의 정보만 알아도 되는 것이다.

 

예를 들어 출발 노드 u와 도착 노드 v가 있을 때, v의 이웃 노드인 x에서 u → x로 갈 때 필요한 c(u, x) 정보를 가지고 있을 것이다. 그러면 도착 노드 v는 이웃 노드 x로부터 얻은 정보를 통해 c(u, x) +  c(x, v)를 계산하여 이중에서 최솟값을 고르면 된다.

그래서 어떤 노드 v는 이웃된 노드 x의 정보만 알고 있으면 바로 계산할 수 있다는 것이 다익스트라 알고리즘과 큰 차이점을 보인다.

 

거기다가 다익스트라 알고리즘은 노드 v가 N'에 속하면 v에 대한 정보는 확정이 되었지만, 벨만-포드 알고리즘은 노드 v에 대한 값이 바뀔 수도 있고, 만약 바뀐다면 다시 새로 계산을 해야한다는 특징이 있다.

 

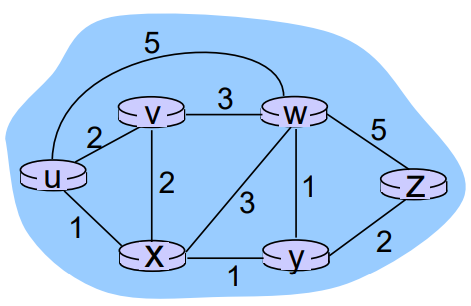
간단하게 예시를 들어보면 시작 노드 u, 도착 노드 z라고 해보자

u의 인접 노드는 v, w, x인데, 어찌어찌 구해서 d_v(z) = 5, d_w(z) = 3 ,d_x(z) = 3를 구했다고 하자

d_u(z) = min{c(u, v) + d_v(z), c(u, w) + d_w(z), c(u, x) + d_x_x(z)} = min{7, 4, 8} = 4가 된다.

 

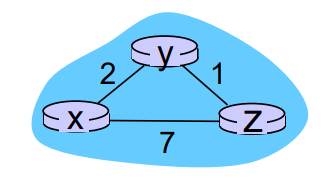
좀 더 이해하기 쉬운 예제를 생각해보자

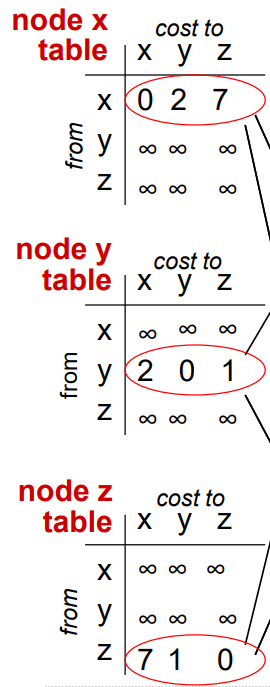
제일 처음에는 노드 x, 노드 y, 노드 z가 전부 자신과 관련된 정보만 가지고 있을 것이다.

 

해당 정보를 다른 노드에게 전달을 하여 테이블을 업데이트한다.

예를 들어 노드 x의 이웃 노드는 노드 y, 노드 z이니 노드 y, z에게 알려준다.

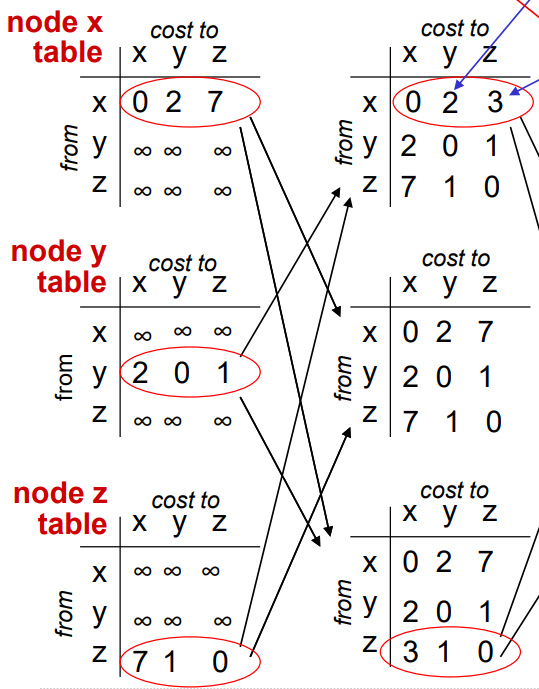
그래서 오른쪽 테이블들처럼 값이 한 번 업데이트가 된다.

이후에 각 노드는 이웃 노드에게 자신이 가진 정보를 알려준다.

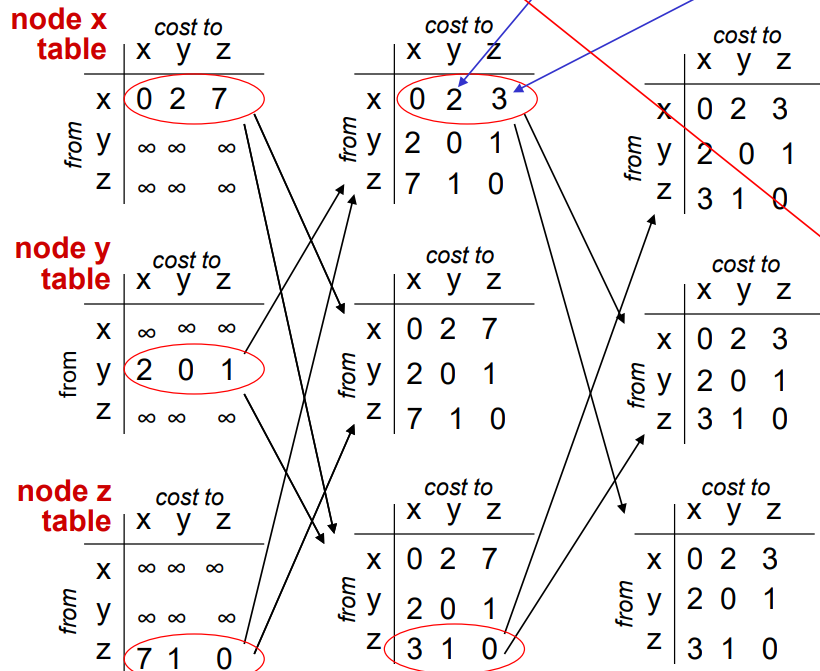
이웃 노드에게 정보를 전달하였고, 테이블 값이 업데이트 된다.

이후 다시 이웃 노드들에게 정보를 전달한다.

하지만 여기서 더 이상 값이 바뀌는게 없으므로 알고리즘은 종료된다.

---